在产品开发设计阶段，为了全面了解产品的可靠性水平，需要对产品的失效数据进行量化分析. 而这就需要对产品进行Test to fail 的试验，然后通过威布尔数据分析方法来计算出当前样本的可靠性数据。好处毋庸置疑，可以比较准确地知道产品的失效信息和可靠性量化数据。但缺点就是，不知道失效什么时候会发生，也许需要很长的时间。

所以，这样的试验安排比较适合于测试计划可以独立于产品项目开发周期的情况。反过来说，通常情况下，在产品开发的不同阶段，可靠性试验的设计都必须满足项目的时间表。因为在每个Milestone Review时，可靠性部门需要给出产品定量或定性的可靠性评估数据。通常做法是 Test to pass 的试验安排。那么，在设计可靠性测试方案时，就需要考虑可靠性的指标是多少，需要多少的测试样品，需要多久的测试时间？这往往是大家比较头疼的事。

这里简单分享一下两个常用的可靠性验证设计方法：基于卡方分布的MTBF定时截尾法，基于二项式分布的参数法。基于二项式分布的非参数法对对于可靠性测试方案设计的意义不大，这里就不予介绍了。

1、基于卡方分布的MTBF定时截尾法

这个方法一般假设了产品的失效分布服从指数分布，所以在电子行业尤其消费电子行业经常被使用。其可靠性指标与样本量、测试时间的关系式可表达如下（单侧置信区间下限）：

这里直接举例来介绍如何权衡试验时间和试验样本量：假设某PC产品的MTBF指标为50000小时，那么测试样品、测试时间，置信度与允许失效数如何计算？一般卡方分布计算时，需要查表，但是可以直接使用EXCEL里CHIINV 函数计算。

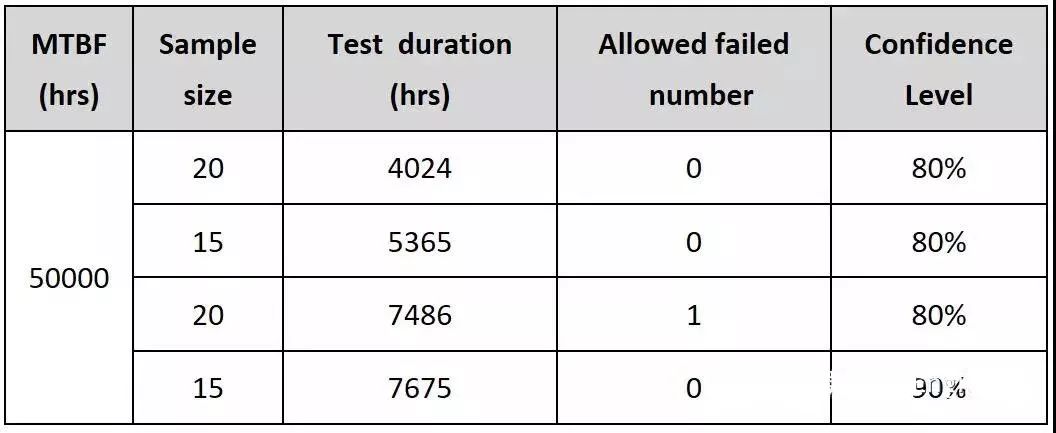
从这张表格可以看出，在指定的MTBF和置信度下，可以通过提高样本量来缩短测试时间，反之，也可以通过增加测试时间来减少样本量。具体如何设定，可以根据实际项目情况来合理安排。

2、基于二项式分布的参数法

第一个方法在使用时，假定了产品的失效服从指数分布，而实际很多产品或零部件的失效是多样性的，有的服从威布尔分布，有的服从正态分布或者对数正态分布。所以第一种方法就不适合表达以上的这些失效分布，取而代之的是基于累积二项式分布的参数计算法。

累积二项式分布的公式表达如下：

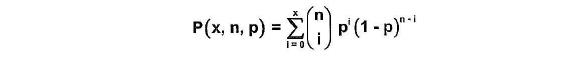
其中，1-p 为R，P(X,n,p)=1-CL，如果，失效数为0时，1-CL=R^n.

由于威布尔分布不同的形参能代表不同的分布类型，所以这里可以结合威布尔的可靠性公式来结合累积二项式分布。具体如下：

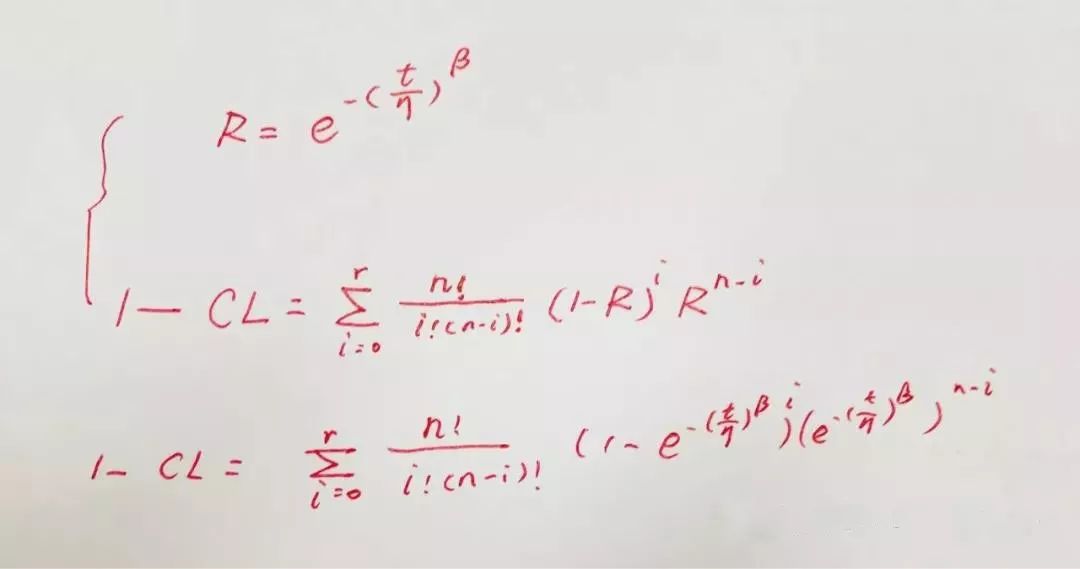
不过计算有点麻烦，可以使用Minitab或者Weibull++里的工具进行计算。如下图所示：

二项式分布参数法，需要提前知道该产品服从威布尔分布的形参Beta，以及该产品的可靠性目标和需要的置信度。形参Beta一般是根据产品或近似产品的历史数据来设定，如某机械部件疲劳失效的形参经验值为3.

可现实情况下，机器人研发往往很多零部件的失效分布的形参是未知的。这就无法通过上述方法来制定可接受的可靠性定量测试。我个人的做法是通过产品设定的不同时间点可靠性指标来计算出一个形参。例如，某产品的目标寿命为10年（按实际工况换算为45000小时）70%的可靠性，置信度为80%；同时还有保证2年内（按实际工况换算为9000小时），累积失效不超过2%。那么，我们就可以根据威布尔可靠性公式来列出方程组，求出相对应的形参和特征寿命：

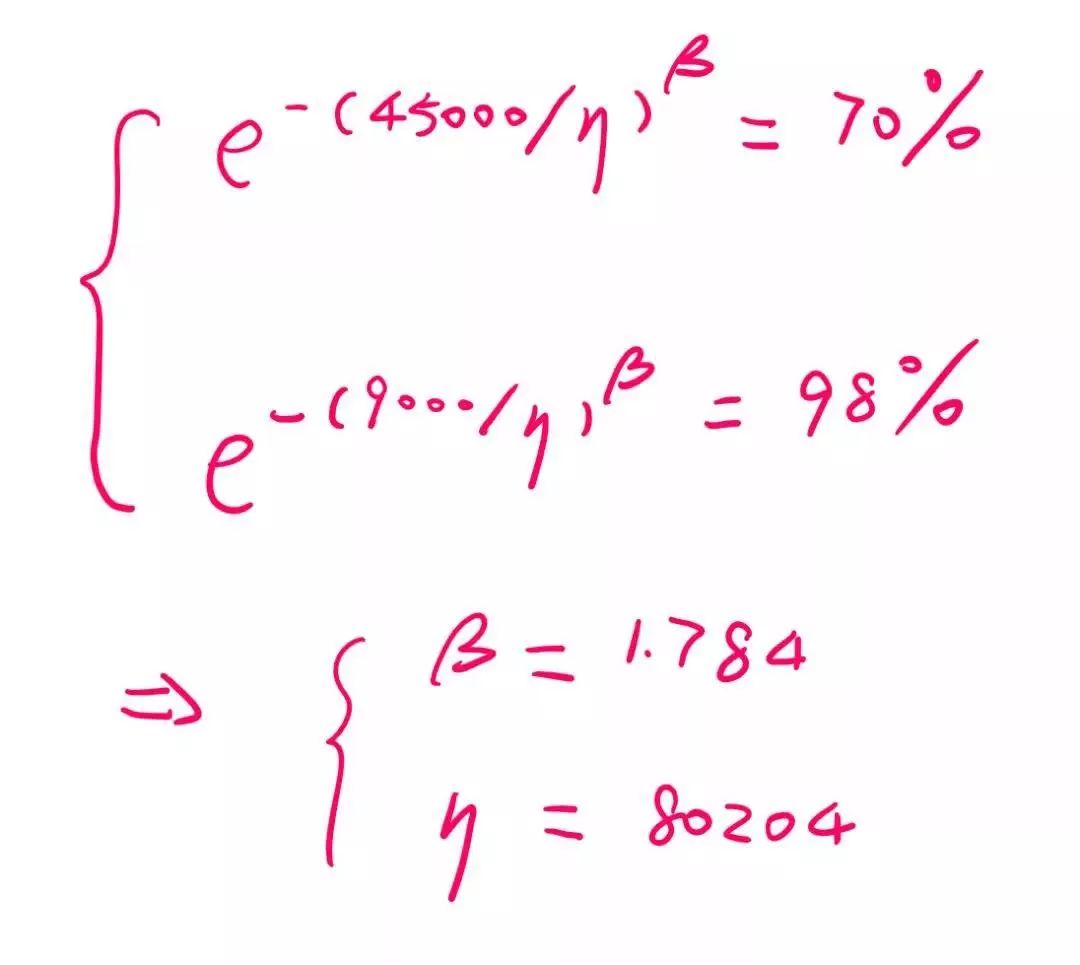
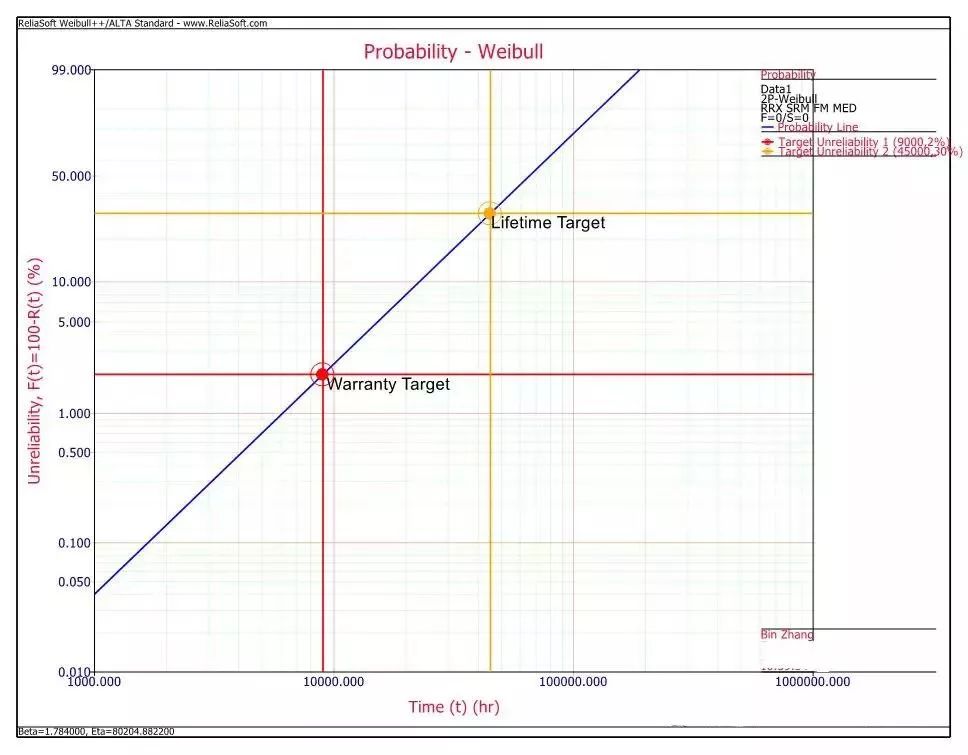
也就是说，如果该产品失效服从威布尔分布，又要同时满足warranty target 和lifetime target的话，那么实际失效数据拟合出的直线需要在基准线的下方(至少lifetime时间点前)。也许实际的产品可靠性数据好于上图的基准数据，这样会在测试上造成一定的时间和样本量的浪费。但是可以确保我们制定的测试方案不会出现没有达到可靠性指标的情况。如果计算出的测试时间还是太长的话，我们还可以通过提高应力来进行加速测试。如下图所示：

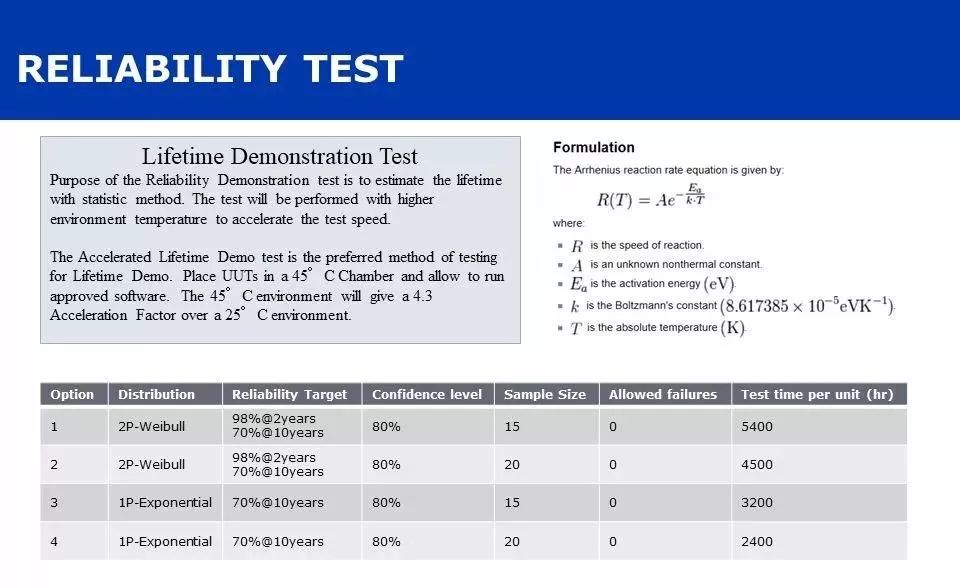
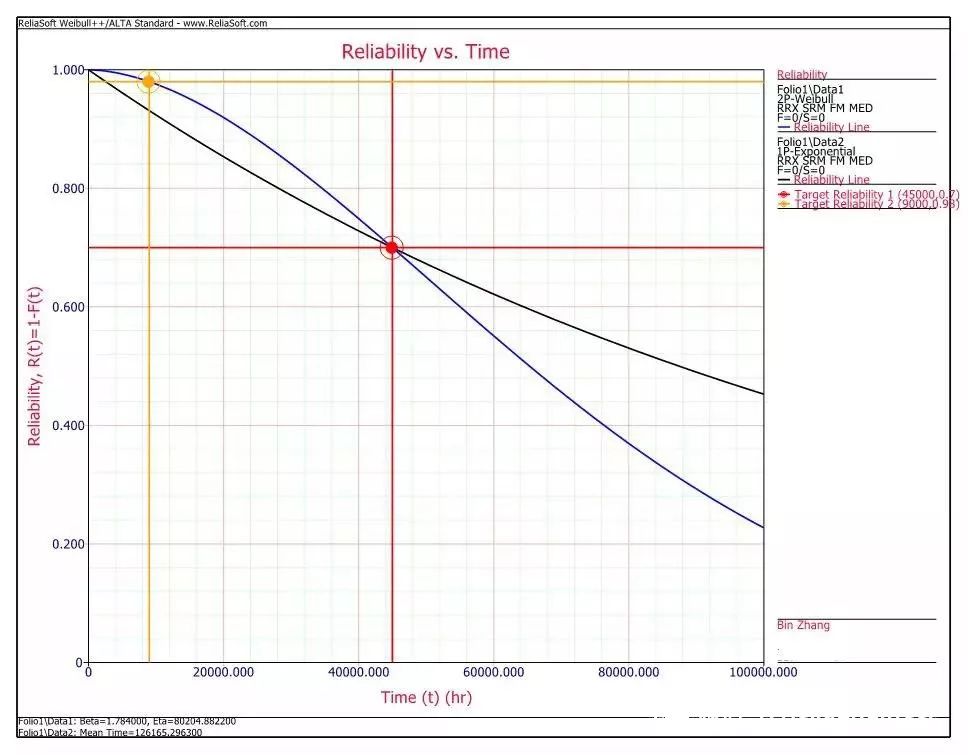
通过上图的对比，可以看出在使用工具设计可靠性测试方案时，尽管寿命目标值一样，但是选择不同的分布类型（考虑了warranty target的两参数威布尔分布）对测试效果还是有显著的区别。

结语

上面简单介绍了机器人技术服务两种常用的可靠性测试方案设计方法，这可以很好得帮我们权衡样品数量和测试时间的关系。但是这两种方法都有一个明显的缺点，那就是如果样本量可以很大的时候，测试时间会变得很短；反之亦然。这两种情况都会都可靠性测试的效果带来严重的影响。个人观点是样本量和测试时间需要适中，如果样本量不是很多的情况下（至少不能少于3个），优先选择延长测试时间。如果测试计算下来还是非常长的，可以通过提高测试应力来进行加速测试。还有就是，设计测试时，允许失效数应尽量为0.

当然，除了上述两种方法外，还有诸如基于贝叶斯的非参数法，这是基于一定经验数据的分析方法。有兴趣的朋友可以参阅相关资料或网页进行了解。